Rumus Trigonometri Sudut Rangkap
Rumus Trigonometri Sudut Rangkap
Seperti yang kita ketahui bahwa, besar sudut yang termasuk dalam sudut istimewa adalah 30o, 45o, 60o, 90o, dan sudut istimewa dengan penambahan secara periodik lainnya. Sedangkan contoh sudut yang bukan merupakan sudut istimewa adalah 75o, 105o, dan lain sebagainya.

Rumus trigonometri sudut rangkap meliputi 3 persamaan fungsi trigonometri. Ketiga persamaan tersebut adalah fungsi sin sudut rangkap, fungsi cos sudut rangkap, dan fungsi tan sudut rangkap.
Rumus Sudut Rangkap Fungsi Sinus
Bahasan pertama adalah rumus sudut rangkap fungsi sinus. Persamaan sudut rangkap untuk fungsi sinus dapat dinyatakan melalui sebuah persamaan, yaitu sin 2 alpha sama dengan 2 dikali sin alpha dikali cos alpha. Rumus sudut rangkap sinus dinyatakan dalam rumus berikut.
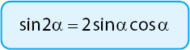
Dari mana fungsi rumus sudut rangkap fungsi sinus di atas diperoleh? Perhatikan pembuktian yang akan diberikan berikut.
Bukti:
Terbukti
Contoh Soal Penggunaan Sudut Rangkap Sinus dan pembahasannya
Jika diketahui:
di mana α merupakan sudut lancip, tentukan nilai sin 2 α!
Pembahasan:
Sehingga,
Rumus Sudut Rangkap Fungsi Cosinus
Ada tiga rumus yang dapat digunakan untuk menentukan nilai sudut rangkap cosinus. Ketiga rumus untuk sudut rangkap fungsi cosinus diberikan seperti tiga persamaan berikut.
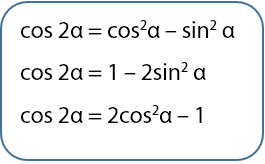
Bukti:
Persamaan pertama:
Selanjutnya akan dibuktikan bahwa persamaan kedua dan ketiga adalah persamaan yang benar.

Sebelum membuktikan kedua rumus lainnya, ingat kembali rumus identitas trigonometri dari persamaan sin2α + cos2α = 1.
Persamaan kedua:
Persamaan ketiga:
Terbukti benar untuk tiga persamaan pada sudut rangkap fungsi cosinus.
Contoh Soal Penggunaan Sudut Rangkap Cosinus dan pembahasannya
Tentukan nilai fungsi cosinus untuk sudut 120o dengan memanfaatkan rumus pada sudut rangkap!
Pembahasan:
Rumus Sudut Rangkap Fungsi Tangen
Ketiga adalah bahasan rumus sudut rangkap untuk fungsi tangen. Terdapat sebuah persamaan yang menyatakan persamaan sudut rangkap fungsi tangen. Rumus sudut rangkap sinus dinyatakan dalam rumus berikut.
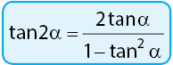
Dari mana persamaan di atas diperoleh? Perhatikan pembuktian berikut.
Bukti:
Terbukti
Contoh Soal Penggunaan Sudut Rangkap Tangen dan Pembahasannya
Jika diketahui nilai
Jika sudut α merupakan sudut lancip maka tentukan nilai tan 2 α.
Pembahasan:
Komentar
Posting Komentar